如何从 FFT 中提取特征?
How to extract features from FFT?
我正在从以 200 Hz 采样的 X、Y 和 Z 加速计传感器收集数据。 3 个轴组合成一个信号,称为 'XYZ_Acc'。我遵循了有关如何使用 scipy fftpack 库将时域信号转换为频域的教程。
我使用的代码如下:
from scipy.fftpack import fft
# get a 500ms slice from dataframe
sample500ms = df.loc[pd.to_datetime('2019-12-15 11:01:31.000'):pd.to_datetime('2019-12-15 11:01:31.495')]['XYZ_Acc']
f_s = 200 # sensor sampling frequency 200 Hz
T = 0.005 # 5 milliseconds between successive observation T =1/f_s
N = 100 # 100 samples in 0.5 seconds
f_values = np.linspace(0.0, f_s/2, N//2)
fft_values = fft(sample500ms)
fft_mag_values = 2.0/N * np.abs(fft_values[0:N//2])
然后我绘制频率与幅度的关系图
fig_fft = plt.figure(figsize=(5,5))
ax = fig_fft.add_axes([0,0,1,1])
ax.plot(f_values,fft_mag_values)
截图:
我现在的困难是如何从这些数据中提取特征,例如不规则性、基频、通量...
有人可以指导我正确的方向吗?
更新 06/01/2019 - 为我的问题添加更多上下文。
我在机器学习方面相对较新,因此欢迎任何反馈。 X、Y、Z 是线性加速度信号,从智能 phone 以 200 Hz 采样。我正在尝试通过分析光谱和时间统计数据来检测道路异常。
这是一个 csv 文件的示例,它被解析为一个 pandas 数据帧,以时间戳为索引。
X,Y,Z,Latitude,Longitude,Speed,timestamp
0.8756,-1.3741,3.4166,35.894833,14.354166,11.38,2019-12-15 11:01:30:750
1.0317,-0.2728,1.5602,35.894833,14.354166,11.38,2019-12-15 11:01:30:755
1.0317,-0.2728,1.5602,35.894833,14.354166,11.38,2019-12-15 11:01:30:760
1.0317,-0.2728,1.5602,35.894833,14.354166,11.38,2019-12-15 11:01:30:765
-0.1669,-1.9912,-4.2043,35.894833,14.354166,11.38,2019-12-15 11:01:30:770
-0.1669,-1.9912,-4.2043,35.894833,14.354166,11.38,2019-12-15 11:01:30:775
-0.1669,-1.9912,-4.2043,35.894833,14.354166,11.38,2019-12-15 11:01:30:780
为了回答 'francis',然后通过以下代码添加两列:
df['XYZ_Acc_Mag'] = (abs(df['X']) + abs(df['Y']) + abs(df['Z']))
df['XYZ_Acc'] = (df['X'] + df['Y'] + df['Z'])
'XYZ_Acc_Mag' 用于提取时间统计数据。
'XYZ_Acc' 用于提取光谱统计信息。
数据 'XYZ_Acc_Mag' 然后以 0.5 秒的频率重新采样,并在新的数据帧中提取时间统计数据,例如均值、标准差等。配对图揭示了上方线图中时间 11:01:35 处显示的异常。
现在回到我原来的问题。我正在重新采样数据 'XYZ_Acc',也是在 0.5 秒处,并获得幅度数组 'fft_mag_values'。问题是如何从中提取不规则性、基频、通量等时间特征?
由于'XYZ_Acc'被定义为信号分量的线性组合,因此对其进行DFT是有意义的。它相当于在方向 (1,1,1) 上使用一维加速度计。但是可以采用更与物理能量相关的观点。
计算 DFT 类似于将信号写为正弦之和。如果加速度向量写成:
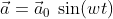
对应的速度矢量可以写成:
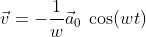
比动能为:
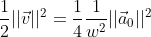
此方法需要在每个频率对应的幅度之前计算每个分量的 DFT。
另一个问题是 DFT 旨在计算周期信号的离散傅立叶变换,该信号是通过对帧进行周期化来构建的。然而,实际帧绝不是周期信号的周期,重复周期会在帧的 end/begin 处人为地产生不连续性。光谱域中的强烈不连续性影响,视为 spectral leakage, could be reduced by windowing 帧。计算实数到复数的 DFT 会产生功率分布,在特定频率处具有峰值。
此外,给定峰值的频率最好估计为相对于功率密度的平均频率,如
所示
另一个估计基频的工具是计算信号的自相关:它在信号周期附近更高。由于信号是 3 个分量的向量,因此可以构建自相关矩阵。它每次都是一个 3x3 厄米特矩阵,因此具有实数特征值。较高特征值的最大值可以表示为振动的幅度,而相应的特征向量是一个复方向,有点类似于振动方向与 angular 偏移量的组合。 angular 偏移量可能表示椭圆体振动。
这是一个假信号,通过添加高斯噪声和正弦波构建:
这是正弦波上重叠的给定帧的功率密度谱:
这里是同帧自相关得到的特征值,可见50Hz正弦波的周期。垂直缩放是错误的:
示例代码如下:
import matplotlib.pyplot as plt
import numpy as np
import scipy.signal
n=2000
t=np.linspace(0.,n/200,num=n,endpoint=False)
# an artificial signal, just for tests
ax=0.3*np.random.normal(0,1.,n)
ay=0.3*np.random.normal(0,1.,n)
az=0.3*np.random.normal(0,1.,n)
ay[633:733]=ay[633:733]+np.sin(2*np.pi*30*t[633:733])
az[433:533]=az[433:533]+np.sin(2*np.pi*50*t[433:533])
#ax=np.sin(2*np.pi*10*t)
#ay=np.sin(2*np.pi*30*t)
#az=np.sin(2*np.pi*50*t)
plt.plot(t,ax, label='x')
plt.plot(t,ay, label='y')
plt.plot(t,az, label='z')
plt.xlabel('t, s')
plt.ylabel('acc, m.s^-2')
plt.legend()
plt.show()
#splitting the sgnal into frames of 0.5s
noiseheight=0.
for i in range(2*(n/200)):
print 'frame', i,' time ', i*0.5, ' s'
framea=np.zeros((100,3))
framea[:,0]=ax[i*100:i*100+100]
framea[:,1]=ay[i*100:i*100+100]
framea[:,2]=az[i*100:i*100+100]
#for that frame, apply window. Factor 2 so that average remains 1.
window = np.hanning(100)
framea[:,0]=framea[:,0]*window*2
framea[:,1]=framea[:,1]*window*2
framea[:,2]=framea[:,2]*window*2
#DFT transform.
hatacc=np.fft.rfft(framea,axis=0, norm=None)
# scaling by length of frame.
hatacc=hatacc/100.
#computing the magnitude : all non-zero frequency are doubled to merge energy in bin N-k exp(-2ik/n) to bin k
accmag=2*(np.abs(hatacc[:,0])*np.abs(hatacc[:,0])+np.abs(hatacc[:,1])*np.abs(hatacc[:,1])+np.abs(hatacc[:,2])*np.abs(hatacc[:,2]))
accmag[0]=accmag[0]*0.5
#first frame says something about noise
if i==0:
noiseheight=2.*np.max(accmag)
if np.max(accmag)>noiseheight:
peaks, peaksdat=scipy.signal.find_peaks(accmag, height=noiseheight)
timestep=0.005
freq= np.fft.fftfreq(100, d=timestep)
#see
# frequencies of peaks are better estimated as mean frequency of peak, with respect to power density
for ind in peaks:
totalweight=accmag[ind-2]+accmag[ind-1]+accmag[ind]+accmag[ind+1]+accmag[ind+2]
totalweightedfreq=accmag[ind-2]*freq[ind-2]+accmag[ind-1]*freq[ind-1]+accmag[ind]*freq[ind]+accmag[ind+1]*freq[ind+1]+accmag[ind+2]*freq[ind+2]
print 'found peak at frequency' , totalweightedfreq/totalweight, ' of height', accmag[ind]
#ploting
plt.plot(freq[0:50],accmag[0:50], label='||acc||^2')
plt.xlabel('frequency, Hz')
plt.ylabel('||acc||^2, m^2.s^-4')
plt.legend()
plt.show()
#another approach to find fundamental frequencies: computing the autocorrelation of the windowed signal and searching for maximums.
#building the autocorellation matrix
autocorr=np.zeros((100,3,3), dtype=complex)
acxfft=np.fft.fft(framea[:,0],axis=0, norm=None)
acyfft=np.fft.fft(framea[:,1],axis=0, norm=None)
aczfft=np.fft.fft(framea[:,2],axis=0, norm=None)
acxfft[0]=0.
acyfft[0]=0.
aczfft[0]=0.
autocorr[:,0,0]=np.fft.ifft(acxfft*np.conj(acxfft),axis=0, norm=None)
autocorr[:,0,1]=np.fft.ifft(acxfft*np.conj(acyfft),axis=0, norm=None)
autocorr[:,0,2]=np.fft.ifft(acxfft*np.conj(aczfft),axis=0, norm=None)
autocorr[:,1,0]=np.fft.ifft(acyfft*np.conj(acxfft),axis=0, norm=None)
autocorr[:,1,1]=np.fft.ifft(acyfft*np.conj(acyfft),axis=0, norm=None)
autocorr[:,1,2]=np.fft.ifft(acyfft*np.conj(aczfft),axis=0, norm=None)
autocorr[:,2,0]=np.fft.ifft(aczfft*np.conj(acxfft),axis=0, norm=None)
autocorr[:,2,1]=np.fft.ifft(aczfft*np.conj(acyfft),axis=0, norm=None)
autocorr[:,2,2]=np.fft.ifft(aczfft*np.conj(aczfft),axis=0, norm=None)
# at a given time, the 3x3 matrix autocorr is Hermitian.
#Its eigenvalues are real, its unitary eigenvectors signals directions of vibrations and phase between components.
autocorreigval=np.zeros((100,3))
autocorreigvec=np.zeros((100,3,3), dtype=complex)
for j in range(100):
autocorreigval[j,:], autocorreigvec[j,:,:]=np.linalg.eigh(autocorr[j,:,:],UPLO='L')
peaks, peaksdat=scipy.signal.find_peaks(autocorreigval[:50,2], 0.3*autocorreigval[0,2])
cleared=np.zeros(len(peaks))
peakperiod=np.zeros(len(peaks))
for j in range(len(peaks)):
totalweight=autocorreigval[peaks[j]-1,2]+autocorreigval[peaks[j],2]+autocorreigval[peaks[j]+1,2]
totalweightedperiod=0.005*(autocorreigval[peaks[j]-1,2]*(peaks[j]-1)+autocorreigval[peaks[j],2]*(peaks[j])+autocorreigval[peaks[j]+1,2]*(peaks[j]+1))
peakperiod[j]=totalweightedperiod/totalweight
#cleared[0]=1.
fundfreq=1
for j in range(len(peaks)):
if cleared[j]==0:
print "found fundamental frequency :", 1.0/(peakperiod[j]), 'eigenvalue', autocorreigval[peaks[j],2],' dir vibration ', autocorreigvec[peaks[j],:,2]
for k in range(j,len(peaks),1):
mm=np.zeros(1)
np.floor_divide(peakperiod[k],peakperiod[j],out=mm)
if ( np.abs(peakperiod[k]-peakperiod[j]*mm[0])< 0.2*peakperiod[j] or np.abs(peakperiod[k]-(peakperiod[j])*(mm[0]+1))< 0.2*peakperiod[j]) :
cleared[k]=fundfreq
#else :
# print k,j,mm[0]
# print peakperiod[k], peakperiod[j]*mm[0], peakperiod[j]*(mm[0]+1) , peakperiod[j]
fundfreq=fundfreq+1
plt.plot(t[i*100:i*100+100],autocorreigval[:,2], label='autocorrelation, large eigenvalue')
plt.plot(t[i*100:i*100+100],autocorreigval[:,1], label='autocorrelation, medium eigenvalue')
plt.plot(t[i*100:i*100+100],autocorreigval[:,0], label='autocorrelation, small eigenvalue')
plt.xlabel('t, s')
plt.ylabel('acc^2, m^2.s^-4')
plt.legend()
plt.show()
输出为:
frame 0 time 0.0 s
frame 1 time 0.5 s
frame 2 time 1.0 s
frame 3 time 1.5 s
frame 4 time 2.0 s
found peak at frequency 50.11249238149811 of height 0.2437842149351196
found fundamental frequency : 50.31467771196368 eigenvalue 47.03344783764712 dir vibration [-0.11441502+0.00000000e+00j 0.0216911 +2.98101624e-18j
-0.9931962 -5.95276353e-17j]
frame 5 time 2.5 s
frame 6 time 3.0 s
found peak at frequency 30.027895460975156 of height 0.3252387031089667
found fundamental frequency : 29.60690406120401 eigenvalue 61.51059682797539 dir vibration [ 0.11384195+0.00000000e+00j -0.98335779-4.34688198e-17j
-0.14158908+3.87566125e-18j]
frame 7 time 3.5 s
found peak at frequency 26.39622018109896 of height 0.042081187689137545
found fundamental frequency : 67.65844834016518 eigenvalue 6.875616417422696 dir vibration [0.8102307 +0.00000000e+00j 0.32697001-8.83058693e-18j
0.48643275-4.76094302e-17j]
frame 8 time 4.0 s
frame 9 time 4.5 s
频率 50Hz 和 30Hz 被捕获为 50.11/50.31Hz 和 30.02/29.60Hz,方向也非常准确。 26.39Hz/67.65Hz 的最后一个特征可能是垃圾,因为它具有两种方法的不同频率和较低的 magnitude/eigenvalue.
关于监测路面以改善维护,我知道我公司有一个项目,叫做Aigle3D。安装在货车后部的激光以毫米级精度以高速公路速度扫描道路。这辆面包车还配备了服务器、摄像头和其他传感器,从而提供了大量关于道路几何形状和缺陷的数据,目前覆盖了数百公里的法国国家公路网。检测和修复早期的小缺陷和裂缝可能会以有限的成本延长道路的预期寿命。如果有用,来自日常用户加速度计的数据确实可以完成监控系统,从而在出现大坑洞时做出更快的反应。
我正在从以 200 Hz 采样的 X、Y 和 Z 加速计传感器收集数据。 3 个轴组合成一个信号,称为 'XYZ_Acc'。我遵循了有关如何使用 scipy fftpack 库将时域信号转换为频域的教程。
我使用的代码如下:
from scipy.fftpack import fft
# get a 500ms slice from dataframe
sample500ms = df.loc[pd.to_datetime('2019-12-15 11:01:31.000'):pd.to_datetime('2019-12-15 11:01:31.495')]['XYZ_Acc']
f_s = 200 # sensor sampling frequency 200 Hz
T = 0.005 # 5 milliseconds between successive observation T =1/f_s
N = 100 # 100 samples in 0.5 seconds
f_values = np.linspace(0.0, f_s/2, N//2)
fft_values = fft(sample500ms)
fft_mag_values = 2.0/N * np.abs(fft_values[0:N//2])
然后我绘制频率与幅度的关系图
fig_fft = plt.figure(figsize=(5,5))
ax = fig_fft.add_axes([0,0,1,1])
ax.plot(f_values,fft_mag_values)
截图:
我现在的困难是如何从这些数据中提取特征,例如不规则性、基频、通量...
有人可以指导我正确的方向吗?
更新 06/01/2019 - 为我的问题添加更多上下文。
我在机器学习方面相对较新,因此欢迎任何反馈。 X、Y、Z 是线性加速度信号,从智能 phone 以 200 Hz 采样。我正在尝试通过分析光谱和时间统计数据来检测道路异常。
这是一个 csv 文件的示例,它被解析为一个 pandas 数据帧,以时间戳为索引。
X,Y,Z,Latitude,Longitude,Speed,timestamp
0.8756,-1.3741,3.4166,35.894833,14.354166,11.38,2019-12-15 11:01:30:750
1.0317,-0.2728,1.5602,35.894833,14.354166,11.38,2019-12-15 11:01:30:755
1.0317,-0.2728,1.5602,35.894833,14.354166,11.38,2019-12-15 11:01:30:760
1.0317,-0.2728,1.5602,35.894833,14.354166,11.38,2019-12-15 11:01:30:765
-0.1669,-1.9912,-4.2043,35.894833,14.354166,11.38,2019-12-15 11:01:30:770
-0.1669,-1.9912,-4.2043,35.894833,14.354166,11.38,2019-12-15 11:01:30:775
-0.1669,-1.9912,-4.2043,35.894833,14.354166,11.38,2019-12-15 11:01:30:780
为了回答 'francis',然后通过以下代码添加两列:
df['XYZ_Acc_Mag'] = (abs(df['X']) + abs(df['Y']) + abs(df['Z']))
df['XYZ_Acc'] = (df['X'] + df['Y'] + df['Z'])
'XYZ_Acc_Mag' 用于提取时间统计数据。
'XYZ_Acc' 用于提取光谱统计信息。
数据 'XYZ_Acc_Mag' 然后以 0.5 秒的频率重新采样,并在新的数据帧中提取时间统计数据,例如均值、标准差等。配对图揭示了上方线图中时间 11:01:35 处显示的异常。
现在回到我原来的问题。我正在重新采样数据 'XYZ_Acc',也是在 0.5 秒处,并获得幅度数组 'fft_mag_values'。问题是如何从中提取不规则性、基频、通量等时间特征?
由于'XYZ_Acc'被定义为信号分量的线性组合,因此对其进行DFT是有意义的。它相当于在方向 (1,1,1) 上使用一维加速度计。但是可以采用更与物理能量相关的观点。 计算 DFT 类似于将信号写为正弦之和。如果加速度向量写成:
对应的速度矢量可以写成:
比动能为:
此方法需要在每个频率对应的幅度之前计算每个分量的 DFT。
另一个问题是 DFT 旨在计算周期信号的离散傅立叶变换,该信号是通过对帧进行周期化来构建的。然而,实际帧绝不是周期信号的周期,重复周期会在帧的 end/begin 处人为地产生不连续性。光谱域中的强烈不连续性影响,视为 spectral leakage, could be reduced by windowing 帧。计算实数到复数的 DFT 会产生功率分布,在特定频率处具有峰值。
此外,给定峰值的频率最好估计为相对于功率密度的平均频率,如
另一个估计基频的工具是计算信号的自相关:它在信号周期附近更高。由于信号是 3 个分量的向量,因此可以构建自相关矩阵。它每次都是一个 3x3 厄米特矩阵,因此具有实数特征值。较高特征值的最大值可以表示为振动的幅度,而相应的特征向量是一个复方向,有点类似于振动方向与 angular 偏移量的组合。 angular 偏移量可能表示椭圆体振动。
这是一个假信号,通过添加高斯噪声和正弦波构建:
这是正弦波上重叠的给定帧的功率密度谱:
这里是同帧自相关得到的特征值,可见50Hz正弦波的周期。垂直缩放是错误的:
示例代码如下:
import matplotlib.pyplot as plt
import numpy as np
import scipy.signal
n=2000
t=np.linspace(0.,n/200,num=n,endpoint=False)
# an artificial signal, just for tests
ax=0.3*np.random.normal(0,1.,n)
ay=0.3*np.random.normal(0,1.,n)
az=0.3*np.random.normal(0,1.,n)
ay[633:733]=ay[633:733]+np.sin(2*np.pi*30*t[633:733])
az[433:533]=az[433:533]+np.sin(2*np.pi*50*t[433:533])
#ax=np.sin(2*np.pi*10*t)
#ay=np.sin(2*np.pi*30*t)
#az=np.sin(2*np.pi*50*t)
plt.plot(t,ax, label='x')
plt.plot(t,ay, label='y')
plt.plot(t,az, label='z')
plt.xlabel('t, s')
plt.ylabel('acc, m.s^-2')
plt.legend()
plt.show()
#splitting the sgnal into frames of 0.5s
noiseheight=0.
for i in range(2*(n/200)):
print 'frame', i,' time ', i*0.5, ' s'
framea=np.zeros((100,3))
framea[:,0]=ax[i*100:i*100+100]
framea[:,1]=ay[i*100:i*100+100]
framea[:,2]=az[i*100:i*100+100]
#for that frame, apply window. Factor 2 so that average remains 1.
window = np.hanning(100)
framea[:,0]=framea[:,0]*window*2
framea[:,1]=framea[:,1]*window*2
framea[:,2]=framea[:,2]*window*2
#DFT transform.
hatacc=np.fft.rfft(framea,axis=0, norm=None)
# scaling by length of frame.
hatacc=hatacc/100.
#computing the magnitude : all non-zero frequency are doubled to merge energy in bin N-k exp(-2ik/n) to bin k
accmag=2*(np.abs(hatacc[:,0])*np.abs(hatacc[:,0])+np.abs(hatacc[:,1])*np.abs(hatacc[:,1])+np.abs(hatacc[:,2])*np.abs(hatacc[:,2]))
accmag[0]=accmag[0]*0.5
#first frame says something about noise
if i==0:
noiseheight=2.*np.max(accmag)
if np.max(accmag)>noiseheight:
peaks, peaksdat=scipy.signal.find_peaks(accmag, height=noiseheight)
timestep=0.005
freq= np.fft.fftfreq(100, d=timestep)
#see
# frequencies of peaks are better estimated as mean frequency of peak, with respect to power density
for ind in peaks:
totalweight=accmag[ind-2]+accmag[ind-1]+accmag[ind]+accmag[ind+1]+accmag[ind+2]
totalweightedfreq=accmag[ind-2]*freq[ind-2]+accmag[ind-1]*freq[ind-1]+accmag[ind]*freq[ind]+accmag[ind+1]*freq[ind+1]+accmag[ind+2]*freq[ind+2]
print 'found peak at frequency' , totalweightedfreq/totalweight, ' of height', accmag[ind]
#ploting
plt.plot(freq[0:50],accmag[0:50], label='||acc||^2')
plt.xlabel('frequency, Hz')
plt.ylabel('||acc||^2, m^2.s^-4')
plt.legend()
plt.show()
#another approach to find fundamental frequencies: computing the autocorrelation of the windowed signal and searching for maximums.
#building the autocorellation matrix
autocorr=np.zeros((100,3,3), dtype=complex)
acxfft=np.fft.fft(framea[:,0],axis=0, norm=None)
acyfft=np.fft.fft(framea[:,1],axis=0, norm=None)
aczfft=np.fft.fft(framea[:,2],axis=0, norm=None)
acxfft[0]=0.
acyfft[0]=0.
aczfft[0]=0.
autocorr[:,0,0]=np.fft.ifft(acxfft*np.conj(acxfft),axis=0, norm=None)
autocorr[:,0,1]=np.fft.ifft(acxfft*np.conj(acyfft),axis=0, norm=None)
autocorr[:,0,2]=np.fft.ifft(acxfft*np.conj(aczfft),axis=0, norm=None)
autocorr[:,1,0]=np.fft.ifft(acyfft*np.conj(acxfft),axis=0, norm=None)
autocorr[:,1,1]=np.fft.ifft(acyfft*np.conj(acyfft),axis=0, norm=None)
autocorr[:,1,2]=np.fft.ifft(acyfft*np.conj(aczfft),axis=0, norm=None)
autocorr[:,2,0]=np.fft.ifft(aczfft*np.conj(acxfft),axis=0, norm=None)
autocorr[:,2,1]=np.fft.ifft(aczfft*np.conj(acyfft),axis=0, norm=None)
autocorr[:,2,2]=np.fft.ifft(aczfft*np.conj(aczfft),axis=0, norm=None)
# at a given time, the 3x3 matrix autocorr is Hermitian.
#Its eigenvalues are real, its unitary eigenvectors signals directions of vibrations and phase between components.
autocorreigval=np.zeros((100,3))
autocorreigvec=np.zeros((100,3,3), dtype=complex)
for j in range(100):
autocorreigval[j,:], autocorreigvec[j,:,:]=np.linalg.eigh(autocorr[j,:,:],UPLO='L')
peaks, peaksdat=scipy.signal.find_peaks(autocorreigval[:50,2], 0.3*autocorreigval[0,2])
cleared=np.zeros(len(peaks))
peakperiod=np.zeros(len(peaks))
for j in range(len(peaks)):
totalweight=autocorreigval[peaks[j]-1,2]+autocorreigval[peaks[j],2]+autocorreigval[peaks[j]+1,2]
totalweightedperiod=0.005*(autocorreigval[peaks[j]-1,2]*(peaks[j]-1)+autocorreigval[peaks[j],2]*(peaks[j])+autocorreigval[peaks[j]+1,2]*(peaks[j]+1))
peakperiod[j]=totalweightedperiod/totalweight
#cleared[0]=1.
fundfreq=1
for j in range(len(peaks)):
if cleared[j]==0:
print "found fundamental frequency :", 1.0/(peakperiod[j]), 'eigenvalue', autocorreigval[peaks[j],2],' dir vibration ', autocorreigvec[peaks[j],:,2]
for k in range(j,len(peaks),1):
mm=np.zeros(1)
np.floor_divide(peakperiod[k],peakperiod[j],out=mm)
if ( np.abs(peakperiod[k]-peakperiod[j]*mm[0])< 0.2*peakperiod[j] or np.abs(peakperiod[k]-(peakperiod[j])*(mm[0]+1))< 0.2*peakperiod[j]) :
cleared[k]=fundfreq
#else :
# print k,j,mm[0]
# print peakperiod[k], peakperiod[j]*mm[0], peakperiod[j]*(mm[0]+1) , peakperiod[j]
fundfreq=fundfreq+1
plt.plot(t[i*100:i*100+100],autocorreigval[:,2], label='autocorrelation, large eigenvalue')
plt.plot(t[i*100:i*100+100],autocorreigval[:,1], label='autocorrelation, medium eigenvalue')
plt.plot(t[i*100:i*100+100],autocorreigval[:,0], label='autocorrelation, small eigenvalue')
plt.xlabel('t, s')
plt.ylabel('acc^2, m^2.s^-4')
plt.legend()
plt.show()
输出为:
frame 0 time 0.0 s
frame 1 time 0.5 s
frame 2 time 1.0 s
frame 3 time 1.5 s
frame 4 time 2.0 s
found peak at frequency 50.11249238149811 of height 0.2437842149351196
found fundamental frequency : 50.31467771196368 eigenvalue 47.03344783764712 dir vibration [-0.11441502+0.00000000e+00j 0.0216911 +2.98101624e-18j
-0.9931962 -5.95276353e-17j]
frame 5 time 2.5 s
frame 6 time 3.0 s
found peak at frequency 30.027895460975156 of height 0.3252387031089667
found fundamental frequency : 29.60690406120401 eigenvalue 61.51059682797539 dir vibration [ 0.11384195+0.00000000e+00j -0.98335779-4.34688198e-17j
-0.14158908+3.87566125e-18j]
frame 7 time 3.5 s
found peak at frequency 26.39622018109896 of height 0.042081187689137545
found fundamental frequency : 67.65844834016518 eigenvalue 6.875616417422696 dir vibration [0.8102307 +0.00000000e+00j 0.32697001-8.83058693e-18j
0.48643275-4.76094302e-17j]
frame 8 time 4.0 s
frame 9 time 4.5 s
频率 50Hz 和 30Hz 被捕获为 50.11/50.31Hz 和 30.02/29.60Hz,方向也非常准确。 26.39Hz/67.65Hz 的最后一个特征可能是垃圾,因为它具有两种方法的不同频率和较低的 magnitude/eigenvalue.
关于监测路面以改善维护,我知道我公司有一个项目,叫做Aigle3D。安装在货车后部的激光以毫米级精度以高速公路速度扫描道路。这辆面包车还配备了服务器、摄像头和其他传感器,从而提供了大量关于道路几何形状和缺陷的数据,目前覆盖了数百公里的法国国家公路网。检测和修复早期的小缺陷和裂缝可能会以有限的成本延长道路的预期寿命。如果有用,来自日常用户加速度计的数据确实可以完成监控系统,从而在出现大坑洞时做出更快的反应。