NumPy 中 exp(-x^2) 的快速傅里叶变换
Fast Fourier Transform of exp(-x^2) in NumPy
我必须计算高斯函数的二阶导数:
我在这里阅读了关于该主题的所有问题,但无法得出好的结果。我选择了 NumPy 作为我的首选工具。
我们教授的指示:
- 获取大小为
N = 128 的 x 数组,步长为 dx = 1。所以,-64, -63, ..., 62, 63。计算f(x)
- 对
f(x) 执行 FFT 并接收转换后的数组 f_m。
f_m乘以 ,其中
,其中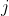 为虚数单位,
为虚数单位,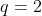 为求导度,
为求导度,

- 执行反向 FFT 以接收导数。
- 在某些 FFT 实现中,您可能必须按
1/n 缩放(但这是现在最小的问题)
下面是我的代码,尽可能简单。
import numpy as np
# Set some parameters
n = 128
dx = 1
a = 0.001
# Create x, calculate f(x) and its FFT
x = np.arange(-n/2, n/2) * dx
psi = np.exp(-a * x * x)
f_m = np.fft.fft(psi)
# k_m creation according to professor (point 3. in my instruction)
k_m = np.arange(-n/2, n/2, dtype=float)
k_m[:int(n / 2)] = (2 * np.pi * k_m[:int(n / 2)]) / (n * dx)
k_m[int(n / 2):] = (2 * np.pi * (k_m[int(n / 2):] - n)) / (n * dx)
# Multiply f_m by (j * k_m)^q. For q=2, this is -k_m^2
f_m *= -k_m * k_m
# Inverse FFT on the result to get the second derivative and scale by 1 / n
f_m = np.fft.ifft(f_m) / n
我无法得到的一件事是结果仍然有虚部,所以有些地方不对。有人可以帮忙吗?
编辑:Cris Luengo 的回答有效。
这部分是错误的:
k_m = np.arange(-n/2, n/2, dtype=float)
第 3 步中的说明讨论了 m 从 0 到 n-1。代码应如下所示:
k_m = np.arange(0, n, dtype=float)
half = int(n / 2) + 1; # notice the + 1 here!
k_m[:half] = (2 * np.pi * k_m[:half]) / (n * dx)
k_m[half:] = (2 * np.pi * (k_m[half:] - n)) / (n * dx)
FFT 产生一个输出,其中第一个元素(索引 0)是 0 频率,而不是频率 -n/2。
如果您使用 fftshift 将 0 频率仓移动到数组的中间,您当前版本的 k_m 数组可能是正确的,尽管我不完全确定这一点(也许下半部分的 -n 应该被删除?)。
最后,这里不需要除以n:
f_m = np.fft.ifft(f_m) / n
NumPy IFFT 已经标准化。
并记得在验证虚部几乎为零后绘制 f_m.real(这些值应该与零不同只是因为数值舍入误差)。
如果您使 a 大一点,例如 a=0.005,那么您的输入高斯分布完全适合输入信号,并且您不会因过滤信号而产生难看的边缘效应被切断了。
您可以使用更简单的 k,只要您在某些时候执行正确的 FT 转换,其实现与您的讲师或@CrisLuengo 明确编写的相同。
import numpy as np
# Set some parameters
n = 128
dx = 1
a = 0.001
# Create x, calculate f(x) and its FFT
x = np.arange(-n // 2, n // 2) * dx
f_x = np.exp(-a * x ** 2)
dd_f_x = 2 * a * np.exp(-a * x ** 2) * (2 * a * x ** 2 - 1)
f_k = np.fft.fft(f_x)
k = np.fft.ifftshift(np.arange(-n // 2, n // 2))
k = (2 * np.pi * k / (n * dx))
dd_f_k = -k ** 2 * f_k
dd_f_x_ = np.fft.ifft(dd_f_k)
按预期工作:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1, squeeze=True)
ax.plot(x, dd_f_x_.real, label='∂²/∂x² f(x) with DFT')
ax.plot(x, dd_f_x, label='∂²/∂x² f(x)')
ax.legend()
我必须计算高斯函数的二阶导数:
我在这里阅读了关于该主题的所有问题,但无法得出好的结果。我选择了 NumPy 作为我的首选工具。
我们教授的指示:
- 获取大小为
N = 128的x数组,步长为dx = 1。所以,-64, -63, ..., 62, 63。计算f(x) - 对
f(x)执行 FFT 并接收转换后的数组f_m。 f_m乘以,其中
为虚数单位,
为求导度,
- 执行反向 FFT 以接收导数。
- 在某些 FFT 实现中,您可能必须按
1/n缩放(但这是现在最小的问题)
下面是我的代码,尽可能简单。
import numpy as np
# Set some parameters
n = 128
dx = 1
a = 0.001
# Create x, calculate f(x) and its FFT
x = np.arange(-n/2, n/2) * dx
psi = np.exp(-a * x * x)
f_m = np.fft.fft(psi)
# k_m creation according to professor (point 3. in my instruction)
k_m = np.arange(-n/2, n/2, dtype=float)
k_m[:int(n / 2)] = (2 * np.pi * k_m[:int(n / 2)]) / (n * dx)
k_m[int(n / 2):] = (2 * np.pi * (k_m[int(n / 2):] - n)) / (n * dx)
# Multiply f_m by (j * k_m)^q. For q=2, this is -k_m^2
f_m *= -k_m * k_m
# Inverse FFT on the result to get the second derivative and scale by 1 / n
f_m = np.fft.ifft(f_m) / n
我无法得到的一件事是结果仍然有虚部,所以有些地方不对。有人可以帮忙吗?
编辑:Cris Luengo 的回答有效。
这部分是错误的:
k_m = np.arange(-n/2, n/2, dtype=float)
第 3 步中的说明讨论了 m 从 0 到 n-1。代码应如下所示:
k_m = np.arange(0, n, dtype=float)
half = int(n / 2) + 1; # notice the + 1 here!
k_m[:half] = (2 * np.pi * k_m[:half]) / (n * dx)
k_m[half:] = (2 * np.pi * (k_m[half:] - n)) / (n * dx)
FFT 产生一个输出,其中第一个元素(索引 0)是 0 频率,而不是频率 -n/2。
如果您使用 fftshift 将 0 频率仓移动到数组的中间,您当前版本的 k_m 数组可能是正确的,尽管我不完全确定这一点(也许下半部分的 -n 应该被删除?)。
最后,这里不需要除以n:
f_m = np.fft.ifft(f_m) / n
NumPy IFFT 已经标准化。
并记得在验证虚部几乎为零后绘制 f_m.real(这些值应该与零不同只是因为数值舍入误差)。
如果您使 a 大一点,例如 a=0.005,那么您的输入高斯分布完全适合输入信号,并且您不会因过滤信号而产生难看的边缘效应被切断了。
您可以使用更简单的 k,只要您在某些时候执行正确的 FT 转换,其实现与您的讲师或@CrisLuengo 明确编写的相同。
import numpy as np
# Set some parameters
n = 128
dx = 1
a = 0.001
# Create x, calculate f(x) and its FFT
x = np.arange(-n // 2, n // 2) * dx
f_x = np.exp(-a * x ** 2)
dd_f_x = 2 * a * np.exp(-a * x ** 2) * (2 * a * x ** 2 - 1)
f_k = np.fft.fft(f_x)
k = np.fft.ifftshift(np.arange(-n // 2, n // 2))
k = (2 * np.pi * k / (n * dx))
dd_f_k = -k ** 2 * f_k
dd_f_x_ = np.fft.ifft(dd_f_k)
按预期工作:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1, squeeze=True)
ax.plot(x, dd_f_x_.real, label='∂²/∂x² f(x) with DFT')
ax.plot(x, dd_f_x, label='∂²/∂x² f(x)')
ax.legend()