逻辑回归中的成本函数给出 NaN 作为结果
Cost function in logistic regression gives NaN as a result
我正在使用批量梯度下降实现逻辑回归。输入样本要分类的有两个类。 类 是 1 和 0。在训练数据时,我使用以下 sigmoid 函数:
t = 1 ./ (1 + exp(-z));
哪里
z = x*theta
我正在使用以下成本函数来计算成本,以确定何时停止训练。
function cost = computeCost(x, y, theta)
htheta = sigmoid(x*theta);
cost = sum(-y .* log(htheta) - (1-y) .* log(1-htheta));
end
我得到的每个步骤的成本都是 NaN,因为在大多数情况下 htheta 的值要么是 1 要么是零。我应该如何确定每次迭代的成本值?
这是逻辑回归的梯度下降代码:
function [theta,cost_history] = batchGD(x,y,theta,alpha)
cost_history = zeros(1000,1);
for iter=1:1000
htheta = sigmoid(x*theta);
new_theta = zeros(size(theta,1),1);
for feature=1:size(theta,1)
new_theta(feature) = theta(feature) - alpha * sum((htheta - y) .*x(:,feature))
end
theta = new_theta;
cost_history(iter) = computeCost(x,y,theta);
end
end
您遇到这种情况可能有两个原因。
数据未规范化
这是因为当您将 sigmoid / logit 函数应用到您的假设时,输出概率几乎全部近似为 0 或全部为 1,并且使用您的成本函数,log(1 - 1) 或 log(0) 将产生-Inf。成本函数中所有这些单独项的累加最终将导致 NaN。
具体来说,如果 y = 0 用于训练示例,并且假设的输出是 log(x),其中 x 是一个非常小的接近于 0 的数字,检查第一个成本函数的一部分会给我们 0*log(x),实际上会产生 NaN。类似地,如果 y = 1 用于训练示例并且假设的输出也是 log(x) 其中 x 是一个非常小的数字,这将再次给我们 0*log(x) 并且将产生 NaN。简单地说,你假设的输出要么非常接近 0,要么非常接近 1。
这很可能是由于每个特征的动态范围差异很大,因此您的假设的一部分,特别是您拥有的每个训练示例的 x*theta 的加权和会给您非常大的负值或正值,如果将 sigmoid 函数应用于这些值,您将非常接近 0 或 1。
解决这个问题的一种方法是 规范化 矩阵中的数据,然后再使用梯度下降进行训练。一种典型的方法是使用 zero-mean 和单位方差进行归一化。给定一个输入特征 x_k 其中 k = 1, 2, ... n 你有 n 个特征,新的规范化特征 x_k^{new} 可以通过以下方式找到:
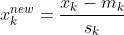
m_k是特征k的均值,s_k是特征k的标准差。这也称为 标准化 数据。您可以在我在这里给出的另一个答案中阅读有关此内容的更多详细信息:
因为您使用线性代数方法进行梯度下降,所以我假设您已经在数据矩阵前面添加了一列全 1。知道这一点,我们可以像这样规范化您的数据:
mX = mean(x,1);
mX(1) = 0;
sX = std(x,[],1);
sX(1) = 1;
xnew = bsxfun(@rdivide, bsxfun(@minus, x, mX), sX);
每个特征的均值和标准差分别存储在mX和sX中。您可以通过阅读我上面链接到您的 post 来了解此代码的工作原理。我不会在这里重复那些东西,因为那不是这个 post 的范围。为确保正确标准化,我将第一列的均值和标准差分别设置为 0 和 1。 xnew 包含新的规范化数据矩阵。将 xnew 与梯度下降算法一起使用。现在,一旦找到参数,要执行任何预测,您 必须 使用来自 训练集 的均值和标准差对任何新测试实例进行归一化。因为学习的参数与训练集的统计数据有关,所以您还必须对要提交给预测模型的任何测试数据应用相同的转换。
假设您有新的数据点存储在一个名为 xx 的矩阵中,您将进行归一化然后执行预测:
xxnew = bsxfun(@rdivide, bsxfun(@minus, xx, mX), sX);
既然你已经有了这个,你就可以进行预测了:
pred = sigmoid(xxnew*theta) >= 0.5;
您可以将 0.5 的阈值更改为您认为最好的值,以决定示例属于正面还是负面 class。
学习率太大
正如您在评论中提到的,一旦您对数据进行归一化,成本似乎是有限的,但在几次迭代后突然变为 NaN。规范化只能让你走到这一步。如果您的学习率或 alpha 太大,每次迭代都会朝最小值的方向过度,从而使每次迭代的成本振荡甚至发散,这似乎正在发生。在您的情况下,成本在每次迭代中都在发散或增加,以至于成本太大以至于无法使用浮点精度表示。
因此,另一种选择是降低学习率 alpha,直到您看到成本函数在每次迭代中都在下降。确定最佳学习率的一种流行方法是对 alpha 的一系列对数间隔值执行梯度下降,然后查看最终成本函数值是多少,然后选择导致最小成本的学习率.
假设成本函数是凸的,结合使用上面的两个事实应该可以让梯度下降很好地收敛。在这种逻辑回归的情况下,它肯定是。
假设您观察到以下情况:
- 真实值为y_i = 1
- 你的模型相当极端并且说 P(y_i = 1) = 1
然后您的成本函数将获得 NaN 的值,因为您要添加 0 * log(0),这是未定义的。因此:
你的成本函数公式有问题(有一个微妙的 0,无穷大问题)!
正如@rayryeng 指出的那样,0 * log(0) 产生了 NaN 因为 0 * Inf 不是犹太洁食。这实际上是一个大问题:如果您的算法认为它可以完美地预测一个值,它会错误地分配 NaN 的成本。
而不是:
cost = sum(-y .* log(htheta) - (1-y) .* log(1-htheta));
您可以通过在 Matlab 中编写成本函数来避免将 0 乘以无穷大:
y_logical = y == 1;
cost = sum(-log(htheta(y_logical))) + sum( - log(1 - htheta(~y_logical)));
想法是,如果 y_i 为 1,我们将 -log(htheta_i) 添加到成本中,但如果 y_i 为 0,我们将 -log(1 - htheta_i) 添加到成本中。这在数学上等同于 -y_i * log(htheta_i) - (1 - y_i) * log(1- htheta_i) 但没有 运行 本质上源于 htheta_i 在双精度浮点数范围内等于 0 或 1 的数值问题。
这件事发生在我身上,因为不确定类型:
0*log(0)
当其中一个预测值 Y 等于 0 或 1 时,就会发生这种情况。
在我的例子中,解决方案是将 if 语句添加到 python 代码中,如下所示:
y * np.log (Y) + (1-y) * np.log (1-Y) if ( Y != 1 and Y != 0 ) else 0
这样,当实际值 (y) 和预测值 (Y) 相等时,不需要计算成本,这是预期的行为。
(注意,当给定的 Y 收敛于 0 时,左加数被取消(因为 y=0),右加数趋向于 0。当 Y 收敛到 1 时会发生同样的情况,但加数相反。)
(还有一种非常罕见的情况,您可能不需要担心,其中 y=0 和 Y=1 反之亦然,但是如果您的数据集是标准化的并且权重正确初始化不会有问题。)
我正在使用批量梯度下降实现逻辑回归。输入样本要分类的有两个类。 类 是 1 和 0。在训练数据时,我使用以下 sigmoid 函数:
t = 1 ./ (1 + exp(-z));
哪里
z = x*theta
我正在使用以下成本函数来计算成本,以确定何时停止训练。
function cost = computeCost(x, y, theta)
htheta = sigmoid(x*theta);
cost = sum(-y .* log(htheta) - (1-y) .* log(1-htheta));
end
我得到的每个步骤的成本都是 NaN,因为在大多数情况下 htheta 的值要么是 1 要么是零。我应该如何确定每次迭代的成本值?
这是逻辑回归的梯度下降代码:
function [theta,cost_history] = batchGD(x,y,theta,alpha)
cost_history = zeros(1000,1);
for iter=1:1000
htheta = sigmoid(x*theta);
new_theta = zeros(size(theta,1),1);
for feature=1:size(theta,1)
new_theta(feature) = theta(feature) - alpha * sum((htheta - y) .*x(:,feature))
end
theta = new_theta;
cost_history(iter) = computeCost(x,y,theta);
end
end
您遇到这种情况可能有两个原因。
数据未规范化
这是因为当您将 sigmoid / logit 函数应用到您的假设时,输出概率几乎全部近似为 0 或全部为 1,并且使用您的成本函数,log(1 - 1) 或 log(0) 将产生-Inf。成本函数中所有这些单独项的累加最终将导致 NaN。
具体来说,如果 y = 0 用于训练示例,并且假设的输出是 log(x),其中 x 是一个非常小的接近于 0 的数字,检查第一个成本函数的一部分会给我们 0*log(x),实际上会产生 NaN。类似地,如果 y = 1 用于训练示例并且假设的输出也是 log(x) 其中 x 是一个非常小的数字,这将再次给我们 0*log(x) 并且将产生 NaN。简单地说,你假设的输出要么非常接近 0,要么非常接近 1。
这很可能是由于每个特征的动态范围差异很大,因此您的假设的一部分,特别是您拥有的每个训练示例的 x*theta 的加权和会给您非常大的负值或正值,如果将 sigmoid 函数应用于这些值,您将非常接近 0 或 1。
解决这个问题的一种方法是 规范化 矩阵中的数据,然后再使用梯度下降进行训练。一种典型的方法是使用 zero-mean 和单位方差进行归一化。给定一个输入特征 x_k 其中 k = 1, 2, ... n 你有 n 个特征,新的规范化特征 x_k^{new} 可以通过以下方式找到:
m_k是特征k的均值,s_k是特征k的标准差。这也称为 标准化 数据。您可以在我在这里给出的另一个答案中阅读有关此内容的更多详细信息:
因为您使用线性代数方法进行梯度下降,所以我假设您已经在数据矩阵前面添加了一列全 1。知道这一点,我们可以像这样规范化您的数据:
mX = mean(x,1);
mX(1) = 0;
sX = std(x,[],1);
sX(1) = 1;
xnew = bsxfun(@rdivide, bsxfun(@minus, x, mX), sX);
每个特征的均值和标准差分别存储在mX和sX中。您可以通过阅读我上面链接到您的 post 来了解此代码的工作原理。我不会在这里重复那些东西,因为那不是这个 post 的范围。为确保正确标准化,我将第一列的均值和标准差分别设置为 0 和 1。 xnew 包含新的规范化数据矩阵。将 xnew 与梯度下降算法一起使用。现在,一旦找到参数,要执行任何预测,您 必须 使用来自 训练集 的均值和标准差对任何新测试实例进行归一化。因为学习的参数与训练集的统计数据有关,所以您还必须对要提交给预测模型的任何测试数据应用相同的转换。
假设您有新的数据点存储在一个名为 xx 的矩阵中,您将进行归一化然后执行预测:
xxnew = bsxfun(@rdivide, bsxfun(@minus, xx, mX), sX);
既然你已经有了这个,你就可以进行预测了:
pred = sigmoid(xxnew*theta) >= 0.5;
您可以将 0.5 的阈值更改为您认为最好的值,以决定示例属于正面还是负面 class。
学习率太大
正如您在评论中提到的,一旦您对数据进行归一化,成本似乎是有限的,但在几次迭代后突然变为 NaN。规范化只能让你走到这一步。如果您的学习率或 alpha 太大,每次迭代都会朝最小值的方向过度,从而使每次迭代的成本振荡甚至发散,这似乎正在发生。在您的情况下,成本在每次迭代中都在发散或增加,以至于成本太大以至于无法使用浮点精度表示。
因此,另一种选择是降低学习率 alpha,直到您看到成本函数在每次迭代中都在下降。确定最佳学习率的一种流行方法是对 alpha 的一系列对数间隔值执行梯度下降,然后查看最终成本函数值是多少,然后选择导致最小成本的学习率.
假设成本函数是凸的,结合使用上面的两个事实应该可以让梯度下降很好地收敛。在这种逻辑回归的情况下,它肯定是。
假设您观察到以下情况:
- 真实值为y_i = 1
- 你的模型相当极端并且说 P(y_i = 1) = 1
然后您的成本函数将获得 NaN 的值,因为您要添加 0 * log(0),这是未定义的。因此:
你的成本函数公式有问题(有一个微妙的 0,无穷大问题)!
正如@rayryeng 指出的那样,0 * log(0) 产生了 NaN 因为 0 * Inf 不是犹太洁食。这实际上是一个大问题:如果您的算法认为它可以完美地预测一个值,它会错误地分配 NaN 的成本。
而不是:
cost = sum(-y .* log(htheta) - (1-y) .* log(1-htheta));
您可以通过在 Matlab 中编写成本函数来避免将 0 乘以无穷大:
y_logical = y == 1;
cost = sum(-log(htheta(y_logical))) + sum( - log(1 - htheta(~y_logical)));
想法是,如果 y_i 为 1,我们将 -log(htheta_i) 添加到成本中,但如果 y_i 为 0,我们将 -log(1 - htheta_i) 添加到成本中。这在数学上等同于 -y_i * log(htheta_i) - (1 - y_i) * log(1- htheta_i) 但没有 运行 本质上源于 htheta_i 在双精度浮点数范围内等于 0 或 1 的数值问题。
这件事发生在我身上,因为不确定类型:
0*log(0)
当其中一个预测值 Y 等于 0 或 1 时,就会发生这种情况。 在我的例子中,解决方案是将 if 语句添加到 python 代码中,如下所示:
y * np.log (Y) + (1-y) * np.log (1-Y) if ( Y != 1 and Y != 0 ) else 0
这样,当实际值 (y) 和预测值 (Y) 相等时,不需要计算成本,这是预期的行为。
(注意,当给定的 Y 收敛于 0 时,左加数被取消(因为 y=0),右加数趋向于 0。当 Y 收敛到 1 时会发生同样的情况,但加数相反。)
(还有一种非常罕见的情况,您可能不需要担心,其中 y=0 和 Y=1 反之亦然,但是如果您的数据集是标准化的并且权重正确初始化不会有问题。)