如何计算聚类熵？工作示例或软件代码
How to calculate clustering entropy? A working example or software code
我想计算这个示例方案的熵
http://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html
任何人都可以用实际值逐步解释吗？我知道有无数的公式，但我真的不擅长理解公式:)
例如在给定的图像中，如何计算纯度得到了清楚而详尽的解释
问题说的很清楚了。我需要一个例子来计算这个聚类方案的熵。可以一步步解释。可以是C#代码或者Phyton代码来计算这样的方案
这里是熵公式
我会用 C# 编写代码
非常感谢您的帮助
我需要这里给出的答案：https://stats.stackexchange.com/questions/95731/how-to-calculate-purity
计算很简单。
概率是 NumberOfMatches/NumberOfCandidates。
您应用 base2 对数并求和。
通常，您会根据集群的相对大小对集群进行加权。
唯一需要注意的是p=0的时候。那么对数是不确定的。但是我们可以安全地使用 p log p = 0 if p = 0 因为 p 在对数之外。
因为log 1 = 0最小熵为0，完美结果必须熵为0，否则出错
我承认 NLP 书的这一部分有点混乱，因为他们没有完全计算集群熵的外部度量，而是专注于单个集群熵计算的计算。相反，我将尝试使用一组更直观的变量，并包括计算总熵外部度量的完整方法。
聚类的总熵为：
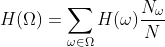
其中：
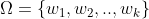是集群的集合
H(w)是单簇熵
N_w是簇中的点数w
N为总点数
簇 w 的熵
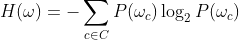
其中：
c是所有分类
的集合C中的一个分类
P(w_c) 是数据点在集群 中被分类为 c 的概率w。
为了使其可用，我们可以将概率替换为该概率的 MLE (maximum likelihood estimate) 以得出：
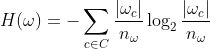
其中：
|w_c| 是聚类 w[= 中分类为 c 的点数79=]
n_w 是簇中的点数 w
所以在给定的示例中，您有 3 个集群（w_1、w_2、w_3），我们将分别计算每个集群的熵，对于这 3 个集群中的每一个分类（x、圆、菱形）。
H(w_1) = (5/6)log_2(5/6) + (1/6)log_2(1/6) + (0/6 )log_2(0/6) = -.650
H(w_2) = (1/6)log_2(1/6) + (4/6)log_2(4/6) + (1/6 )log_2(1/6) = -1.252
H(w_3) = (2/5)log_2(2/5) + (0/5)log_2(0/5) + (3/5 )log_2(3/5) = -.971
因此，要找到一组簇的总熵，您需要将熵的总和乘以每个簇的相对权重。
H(欧米茄) = (-.650 * 6/17) + (-1.252 * 6/17) + (-.971 * 5/17)
H(欧米茄) = -.956
希望对您有所帮助，欢迎大家验证反馈。
我想计算这个示例方案的熵
http://nlp.stanford.edu/IR-book/html/htmledition/evaluation-of-clustering-1.html
任何人都可以用实际值逐步解释吗？我知道有无数的公式，但我真的不擅长理解公式:)
例如在给定的图像中，如何计算纯度得到了清楚而详尽的解释
问题说的很清楚了。我需要一个例子来计算这个聚类方案的熵。可以一步步解释。可以是C#代码或者Phyton代码来计算这样的方案
这里是熵公式
我会用 C# 编写代码
非常感谢您的帮助
我需要这里给出的答案：https://stats.stackexchange.com/questions/95731/how-to-calculate-purity
计算很简单。
概率是 NumberOfMatches/NumberOfCandidates。
您应用 base2 对数并求和。
通常，您会根据集群的相对大小对集群进行加权。
唯一需要注意的是p=0的时候。那么对数是不确定的。但是我们可以安全地使用 p log p = 0 if p = 0 因为 p 在对数之外。
因为log 1 = 0最小熵为0，完美结果必须熵为0，否则出错
我承认 NLP 书的这一部分有点混乱，因为他们没有完全计算集群熵的外部度量，而是专注于单个集群熵计算的计算。相反，我将尝试使用一组更直观的变量，并包括计算总熵外部度量的完整方法。
聚类的总熵为：
其中：
是集群的集合
H(w)是单簇熵
N_w是簇中的点数w
N为总点数
簇 w 的熵
其中： c是所有分类
的集合C中的一个分类P(w_c) 是数据点在集群 中被分类为 c 的概率w。
为了使其可用，我们可以将概率替换为该概率的 MLE (maximum likelihood estimate) 以得出：
其中：
|w_c| 是聚类 w[= 中分类为 c 的点数79=]
n_w 是簇中的点数 w
所以在给定的示例中，您有 3 个集群（w_1、w_2、w_3），我们将分别计算每个集群的熵，对于这 3 个集群中的每一个分类（x、圆、菱形）。
H(w_1) = (5/6)log_2(5/6) + (1/6)log_2(1/6) + (0/6 )log_2(0/6) = -.650
H(w_2) = (1/6)log_2(1/6) + (4/6)log_2(4/6) + (1/6 )log_2(1/6) = -1.252
H(w_3) = (2/5)log_2(2/5) + (0/5)log_2(0/5) + (3/5 )log_2(3/5) = -.971
因此，要找到一组簇的总熵，您需要将熵的总和乘以每个簇的相对权重。
H(欧米茄) = (-.650 * 6/17) + (-1.252 * 6/17) + (-.971 * 5/17)
H(欧米茄) = -.956
希望对您有所帮助，欢迎大家验证反馈。