神经网络:计算隐藏层的误差
Neural Nets: Calculating Error In Hidden Layers
我是神经网络的新手,正在尝试构建一个具有 1 个以上隐藏层的超简单神经网络。
在神经网络的训练阶段调整权重时,调整权重的程度部分取决于"how much error"这个神经元对下一层神经元的贡献。因此,我们需要知道下一层的误差。
只有 1 个隐藏层,计算起来很简单,因为我们的训练数据已经为我们提供了预期的输出,所以我们只需要使用输出层(简单地说,target-out)。当有多个隐藏层时,计算误差变得非常重要。也就是说,如果我们有 10 个隐藏层,而我们在第 5 层,我们怎么知道第 6 层的错误是多少?
谢谢
假设我们的 NN 输出值 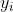 和实际地面实况
和实际地面实况 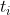 通过损失函数相关,例如, 均方误差(回归案例):
通过损失函数相关,例如, 均方误差(回归案例):
%5E2)
其中:
&space;%5C%5C&space;a_%7B%5Cell&space;-&space;1%7D&space;&=&space;f_%7B%5Cell-1%7D(W_%7B%5Cell-1%7Da_%7B%5Cell&space;-&space;2%7D&space;+&space;b_%7B%5Cell-1%7D)&space;%5C%5C&space;%5Cvdots&space;%5C%5C&space;a_%7B1%7D&space;=&space;f_1(W_1a_0&space;+&space;b_1)&space;%5C%5C&space;a_%7B0%7D&space;=&space;x)
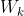 和
和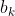 是层
是层 的权重,
的权重,) 是应用于同一层所有神经元反应的激活函数。
是应用于同一层所有神经元反应的激活函数。
为了从输出层传播模型权重的误差,我们可以简单地在误差损失函数和依赖于模型参数(权重或偏差)的因子之间应用链式法则。例如,让我们找到与损失函数和输出层权重相关的误差导数: 如下:
如下:


&space;a_%7B%5Cell&space;-&space;1%7D%5E%7BT%7D&space;%5C%5C)
正如您可以推断的那样,我们可以应用相同的程序来计算误差导数,通过每次激活 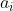 直到网络的较低层。例如,让我们将错误反向传播到层
直到网络的较低层。例如,让我们将错误反向传播到层  :
:


&space;a_%7B%5Cell&space;-&space;2%7D%5E%7BT%7D&space;%5C%5C)
这个过程也可以应用于偏置,直到输入层之前的层 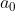 。
。
我希望这个反向传播总结能让您对神经网络的实际实现有一些实际的了解,在这种情况下,前馈神经网络。如果你想了解更多关于反向传播的详细信息,我邀请你查阅斯坦福大学的 UFLDL tutorial on backpropagation:
此外,如果你想了解更适合计算机视觉应用的卷积神经网络,我推荐CS231n课程笔记(其中也有关于反向传播的课程),它们可以在here.
我是神经网络的新手,正在尝试构建一个具有 1 个以上隐藏层的超简单神经网络。
在神经网络的训练阶段调整权重时,调整权重的程度部分取决于"how much error"这个神经元对下一层神经元的贡献。因此,我们需要知道下一层的误差。
只有 1 个隐藏层,计算起来很简单,因为我们的训练数据已经为我们提供了预期的输出,所以我们只需要使用输出层(简单地说,target-out)。当有多个隐藏层时,计算误差变得非常重要。也就是说,如果我们有 10 个隐藏层,而我们在第 5 层,我们怎么知道第 6 层的错误是多少?
谢谢
假设我们的 NN 输出值 和实际地面实况
通过损失函数相关,例如, 均方误差(回归案例):
其中:
和
是层
的权重,
是应用于同一层所有神经元反应的激活函数。
为了从输出层传播模型权重的误差,我们可以简单地在误差损失函数和依赖于模型参数(权重或偏差)的因子之间应用链式法则。例如,让我们找到与损失函数和输出层权重相关的误差导数: 如下:
正如您可以推断的那样,我们可以应用相同的程序来计算误差导数,通过每次激活 直到网络的较低层。例如,让我们将错误反向传播到层
:
这个过程也可以应用于偏置,直到输入层之前的层 。
我希望这个反向传播总结能让您对神经网络的实际实现有一些实际的了解,在这种情况下,前馈神经网络。如果你想了解更多关于反向传播的详细信息,我邀请你查阅斯坦福大学的 UFLDL tutorial on backpropagation:
此外,如果你想了解更适合计算机视觉应用的卷积神经网络,我推荐CS231n课程笔记(其中也有关于反向传播的课程),它们可以在here.