正确的排名损失实施
Correct Ranking Loss Implementation
我有一个 multi-label 问题,我正在尝试将排名损失作为 TensorFlow 中的自定义损失来实现。 (https://arxiv.org/pdf/1312.4894.pdf)
我制作了一个简单的 CNN,带有最终的 Sigmoid 激活层,每个 class 都有独立的分布。
数学公式将标签分成两组,正组和负组。
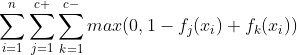
我的问题是,正确的实施方式是什么?
def ranking_loss(y_true, y_pred):
pos = tf.where(tf.equal(y_true, 1), y_pred, tf.zeros_like(y_pred))
neg = tf.where(tf.equal(y_true, 0), y_pred, tf.zeros_like(y_pred))
loss = tf.maximum(1.0 - tf.math.reduce_sum(pos) + tf.math.reduce_sum(neg), 0.0)
return tf.math.reduce_sum(loss)
结果是,对于每个样本,来自正面和负面 classes 的激活分数独立求和。
tr = [1, 0, 0, 1]
pr = [0, 0.6, 0.55, 0.9]
t = tf.constant([tr])
p = tf.constant([pr])
print(ranking_loss(t, p))
tf.Tensor([[0. 0. 0. 0.9]], shape=(1, 4), dtype=float32) #Pos
tf.Tensor([[0. 0.6 0.55 0. ]], shape=(1, 4), dtype=float32) #Neg
tf.Tensor(1.2500001, shape=(), dtype=float32) #loss
CNN 的准确率、召回率和 F1 性能都很差。
改用标准二进制 Cross-Entropy 损失会产生良好的性能,让我觉得我的实现有问题。
我认为根据公式展开总和是不正确的,总和 tf.math.reduce_sum(pos) 和 tf.math.reduce_sum(neg) 不能推入 tf.maximum。如我所见,您的示例的公式将扩展为:
max(0, 1-0+0.6) + max(0, 1-0+0.55) + max(0, 1-0.9+0.6) + max(0, 1-0.9+0.55) = 4.5
你在评论部分提供的第二个实现对我来说很合理,并产生了我预期的结果。但是,让我提供一个替代方案:
def ranking_loss(y_true, y_pred):
y_true_ = tf.cast(y_true, tf.float32)
partial_losses = tf.maximum(0.0, 1 - y_pred[:, None, :] + y_pred[:, :, None])
loss = partial_losses * y_true_[:, None, :] * (1 - y_true_[:, :, None])
return tf.reduce_sum(loss)
这个实现可能更快。
我有一个 multi-label 问题,我正在尝试将排名损失作为 TensorFlow 中的自定义损失来实现。 (https://arxiv.org/pdf/1312.4894.pdf)
我制作了一个简单的 CNN,带有最终的 Sigmoid 激活层,每个 class 都有独立的分布。
数学公式将标签分成两组,正组和负组。
我的问题是,正确的实施方式是什么?
def ranking_loss(y_true, y_pred):
pos = tf.where(tf.equal(y_true, 1), y_pred, tf.zeros_like(y_pred))
neg = tf.where(tf.equal(y_true, 0), y_pred, tf.zeros_like(y_pred))
loss = tf.maximum(1.0 - tf.math.reduce_sum(pos) + tf.math.reduce_sum(neg), 0.0)
return tf.math.reduce_sum(loss)
结果是,对于每个样本,来自正面和负面 classes 的激活分数独立求和。
tr = [1, 0, 0, 1]
pr = [0, 0.6, 0.55, 0.9]
t = tf.constant([tr])
p = tf.constant([pr])
print(ranking_loss(t, p))
tf.Tensor([[0. 0. 0. 0.9]], shape=(1, 4), dtype=float32) #Pos
tf.Tensor([[0. 0.6 0.55 0. ]], shape=(1, 4), dtype=float32) #Neg
tf.Tensor(1.2500001, shape=(), dtype=float32) #loss
CNN 的准确率、召回率和 F1 性能都很差。
改用标准二进制 Cross-Entropy 损失会产生良好的性能,让我觉得我的实现有问题。
我认为根据公式展开总和是不正确的,总和 tf.math.reduce_sum(pos) 和 tf.math.reduce_sum(neg) 不能推入 tf.maximum。如我所见,您的示例的公式将扩展为:
max(0, 1-0+0.6) + max(0, 1-0+0.55) + max(0, 1-0.9+0.6) + max(0, 1-0.9+0.55) = 4.5
你在评论部分提供的第二个实现对我来说很合理,并产生了我预期的结果。但是,让我提供一个替代方案:
def ranking_loss(y_true, y_pred):
y_true_ = tf.cast(y_true, tf.float32)
partial_losses = tf.maximum(0.0, 1 - y_pred[:, None, :] + y_pred[:, :, None])
loss = partial_losses * y_true_[:, None, :] * (1 - y_true_[:, :, None])
return tf.reduce_sum(loss)
这个实现可能更快。