Numpy returns 解析函数的意外结果
Numpy returns unexpected results of analytical function
当我尝试计算下面定义的 d_j(x) 时,基于 Numpy 的算法会产生意外的值。我相信这与数值精度有关,但我不确定如何解决这个问题。
函数为:
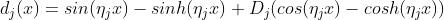
哪里
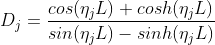
和
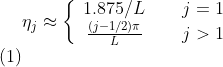
代码在 j>10 时失败。例如,当 j=16 时,函数 d_j(x) returns 来自 x=1 附近的错误值,而预期结果是平滑的、几乎周期性的曲线。
0<x<1.5 图表:
密码是:
#%%
import numpy as np
import matplotlib.pyplot as plt
#%%
L = 1.5 # Length [m]
def eta(j):
if j == 1:
return 1.875 / L
if j > 1:
return (j - 0.5) * np.pi / L
def D(etaj):
etajL = etaj * L
return (np.cos(etajL) + np.cosh(etajL)) / (np.sin(etajL) - np.sinh(etajL))
def d(x, etaj):
etajx = etaj * x
return np.sin(etajx) - np.sinh(etajx) + D(etaj) * (np.cos(etajx) - np.cosh(etajx))
#%%
aux = np.linspace(0, L, 2000)
plt.plot(aux, d(aux, eta(16)))
plt.show()
TL;DR: 问题来自 numerical instabilities.
首先,这是一个简化的代码,它出现了完全相同的问题(具有不同的值):
x = np.arange(0, 50, 0.1)
plt.plot(np.sin(x) - np.sinh(x) - np.cos(x) + np.cosh(x))
plt.show()
这是另一个 没有 出现问题的例子:
x = np.arange(0, 50, 0.1)
plt.plot((np.sin(x) - np.cos(x)) + (np.cosh(x) - np.sinh(x)))
plt.show()
虽然这两个代码在数学上等价于实数,但由于固定大小的浮点精度,它们并不等价。实际上,当 x 比 np.sin(x) 和 np.cos(x) 大 时,np.sinh(x) 和 np.cosh(x) 都会产生巨大的值 。不幸的是,当两个固定大小的浮点数相加时,会损失精度。当添加数字的数量级非常不同时,精度损失可能是巨大的(如果不是关键的话)。例如,在 Python 和主流平台上(因此对于 IEEE-754 64 位浮点数),由于数字表示的精度有限,0.1 + 1e20 == 1e20 为真。因此 (0.1 + 1e20) - 1e20 == 0.0 也为真,而 0.1 + (1e20 - 1e20) == 0.0 不为真(结果值为 0.1)。 浮点加法既不是关联的也不是交换的。在这种特定情况下,准确性可以达到阈值,结果中不再有显着数字。有关浮点精度的更多信息,请阅读 this post。
重点是您在减去浮点数时应该非常小心。一个好的解决方案是放置括号,以便 added/subtracted 值具有相同的数量级。可变大小和更高的精度也有一点帮助。然而,最好的解决方案是analyses the numerical stability of your algorithm. For example, studying condition number在你的算法中使用的数值运算是一个好的开始。
这里比较好的解决办法就是用第二个代码代替第一个。
使用:
aux = np.linspace(0, L, 2000).astype(np.longdouble)
稍微好一点
当我尝试计算下面定义的 d_j(x) 时,基于 Numpy 的算法会产生意外的值。我相信这与数值精度有关,但我不确定如何解决这个问题。
函数为:
哪里
和
代码在 j>10 时失败。例如,当 j=16 时,函数 d_j(x) returns 来自 x=1 附近的错误值,而预期结果是平滑的、几乎周期性的曲线。
0<x<1.5 图表:
密码是:
#%%
import numpy as np
import matplotlib.pyplot as plt
#%%
L = 1.5 # Length [m]
def eta(j):
if j == 1:
return 1.875 / L
if j > 1:
return (j - 0.5) * np.pi / L
def D(etaj):
etajL = etaj * L
return (np.cos(etajL) + np.cosh(etajL)) / (np.sin(etajL) - np.sinh(etajL))
def d(x, etaj):
etajx = etaj * x
return np.sin(etajx) - np.sinh(etajx) + D(etaj) * (np.cos(etajx) - np.cosh(etajx))
#%%
aux = np.linspace(0, L, 2000)
plt.plot(aux, d(aux, eta(16)))
plt.show()
TL;DR: 问题来自 numerical instabilities.
首先,这是一个简化的代码,它出现了完全相同的问题(具有不同的值):
x = np.arange(0, 50, 0.1)
plt.plot(np.sin(x) - np.sinh(x) - np.cos(x) + np.cosh(x))
plt.show()
这是另一个 没有 出现问题的例子:
x = np.arange(0, 50, 0.1)
plt.plot((np.sin(x) - np.cos(x)) + (np.cosh(x) - np.sinh(x)))
plt.show()
虽然这两个代码在数学上等价于实数,但由于固定大小的浮点精度,它们并不等价。实际上,当 x 比 np.sin(x) 和 np.cos(x) 大 时,np.sinh(x) 和 np.cosh(x) 都会产生巨大的值 。不幸的是,当两个固定大小的浮点数相加时,会损失精度。当添加数字的数量级非常不同时,精度损失可能是巨大的(如果不是关键的话)。例如,在 Python 和主流平台上(因此对于 IEEE-754 64 位浮点数),由于数字表示的精度有限,0.1 + 1e20 == 1e20 为真。因此 (0.1 + 1e20) - 1e20 == 0.0 也为真,而 0.1 + (1e20 - 1e20) == 0.0 不为真(结果值为 0.1)。 浮点加法既不是关联的也不是交换的。在这种特定情况下,准确性可以达到阈值,结果中不再有显着数字。有关浮点精度的更多信息,请阅读 this post。
重点是您在减去浮点数时应该非常小心。一个好的解决方案是放置括号,以便 added/subtracted 值具有相同的数量级。可变大小和更高的精度也有一点帮助。然而,最好的解决方案是analyses the numerical stability of your algorithm. For example, studying condition number在你的算法中使用的数值运算是一个好的开始。
这里比较好的解决办法就是用第二个代码代替第一个。
使用:
aux = np.linspace(0, L, 2000).astype(np.longdouble)
稍微好一点