线性化嵌套 for 循环
Linearize nested for loops
我正在研究一些繁重的算法,现在我正试图让它成为多线程的。它有一个带有 2 个嵌套循环的循环:
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
for (int k = j + 1; k < n; ++k) {
function(i, j, k);
}
}
}
我知道,function 次调用的次数将等于
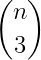
但我还有最后一个问题:我不知道如何根据 b (0 <= b < binom(n, 3) 计算 i、j 和 k )
for (int b = start; b < end; ++b) {
// how to calculate i, j, k?
}
如何计算这些值?
编辑:
我的主要想法是从不同的线程调用这样的函数:
void calculate(int start, int end) {
for (int b = start; b < end; ++b) {
int i = ...;
int j = ...;
int k = ...;
function(i, j, k);
}
}
int total = binom(n, 3);
// thread A:
calculate(0, total / 2);
// thread B:
calculate(total / 2, total);
第三次尝试:
我已经获取了您的代码,并最终将其正确地发送到 运行(在 python 中):
def get_k(n):
total = 0
for i in range(3, n):
for j in range(i + 1, n):
for k in range(j + 1, n):
total += 1
V = total // 2 # for 2 threads
V_tmp = 0
for i in range(3, n):
if(V_tmp > V):
return i
for j in range(i + 1, n):
for k in range(j + 1, n):
V_tmp += 1
def pseudo_thread(start, end, n):
counter = 0
for i in range(start, end):
for j in range(i + 1, n):
for k in range(j + 1, n):
counter += 1
print(counter)
n = 145
k = get_k(n)
pseudo_thread(3, k, n)
pseudo_thread(k, n, n)
这应该最终会给你一个相对较好的拆分。即使 n=145,我们的计数器值也会得到 239260 和 227920。这显然不是一个优雅的解决方案,也不完美,但它在没有太多参考详细数学的情况下给了你正确的答案。
在 中,我分享了一个名为 multi_index 的 class,它基本上可以满足您的需求,即
for(auto m : multi_index(3,3,4))
{
// now m[i] holds index of i-th loop
// m[0] goes from 0 to 2
// m[1] goes from 0 to 2
// m[2] goes from 0 to 3
std::cout<<m[0]<<" "<<m[1]<<" "<<m[2]<<std::endl;
}
但是,此代码仅适用于“正常”循环,其中每个维度从 0 到某个上限值。
在这个 post 中,我将尝试将其应用于反对称情况,其中 m[i]<m[j] 对应 i<j。链接代码的基本思想保持不变,即创建一个 class 来保存循环边界并提供可与基于范围的 for 循环一起使用的迭代器。唯一的区别是我使用 std::vector 而不是 std::array 作为索引数组类型:
#include <iostream>
#include <numeric>
#include <vector>
struct antisym_index_t
{
int upper_index;
int dim;
antisym_index_t(int upper_index, int dim) : upper_index(upper_index), dim(dim) {}
struct iterator
{
struct sentinel_t {};
int upper_index;
int dim;
std::vector<int> index_array = {};
bool _end = false;
iterator(int upper_index, int dim) : upper_index(upper_index), dim(dim), index_array(dim)
{
std::iota(std::begin(index_array), std::end(index_array),0);
}
auto& operator++()
{
for (int i = dim-1;i >= 0;--i)
{
if (index_array[i] < upper_index - 1 - (dim-1-i))
{
++index_array[i];
for (int j = i+1;j < dim;++j)
{
index_array[j] = index_array[j-1]+1;
}
return *this;
}
}
_end = true;
return *this;
}
auto& operator*()
{
return index_array;
}
bool operator!=(sentinel_t) const
{
return !_end;
}
};
auto begin() const
{
return iterator{ upper_index, dim };
}
auto end() const
{
return typename iterator::sentinel_t{};
}
};
auto antisym_index(int upper_index, int dim)
{
return antisym_index_t(upper_index, dim);
}
但是请注意,此代码到目前为止未经测试(写在我的头上)。您可以将其用作
for(auto m : antisym_index(5,3))
{
// now m[i] holds index of i-th loop
std::cout<<m[0]<<" "<<m[1]<<" "<<m[2]<<std::endl;
}
编辑:到目前为止,我已经测试并更正了代码,请参阅 here。给自己的备忘录:不要发布未经测试的代码。
EDIT2:顺便说一句,这在问题中回答了你的问题。我不清楚这对多任务处理有何帮助。
我没有完整的答案,但有 2 个循环的解决方案。我睡眠不足的头脑无法将其概括为 3 个循环,但也许其他人可以。
在 2D 中,问题变成了从展平索引中计算出三角矩阵的行和列索引。这使得很容易看出“逐渐变细”的一端包含在较大的一端中。在 ASCII 艺术中是这样的:
n
___________
|_ |
| |_ |
| |_ |
| | |_ |
| | |_ |
|___|_____|_|
i ^
|
binom(n-i, 2)
所以,让我们定义
n循环结束索引(矩阵数rows/columns)i 外循环计数器范围 [0, n)。如图所示:列索引j 内循环计数器范围 [0, i)。如图:行索引自下而上a 扁平循环计数器范围 [0, binom(n, 2))
然后i可以从binom(n, 2) - binom(n-i, 2) = a计算出来。通过 Wolfram Alpha 的一次往返行程给我们:
i = trunc(-0.5 * sqrt((1 - 2 n)**2 - 8 a) + n - 0.5).
截断(=转换为 int)“向下舍入”到最后一个完整列。所以行索引 j 可以从 as
计算出来
j = a - (binom(n, 2) - binom(n-i, 2))j = a - i*(-i + 2 n - 1) / 2
根据您想要的并行化方式,您还可以使用原子结构并通过比较和交换操作实现迭代。大多数平台上都有一个 16 字节的 CAS。 Link 与 -latomic 在 GCC 上。如果我们确保正确对齐,Clang 会内联 CAS 调用。
#include <atomic>
#include <type_traits>
#include <cstdio>
/**
* Index for a nested loop
*
* Index for loop in style
* for(i = 0; i < n; ++i)
* for(j = 0; j < i; ++j)
* for(k = 0; k < j; ++k);
*
* The total number of iterations is binom(n, 3)
*
* Indices are int for two reasons:
* 1. Keep overall size at or below 16 byte to allow atomic operations
* 2. The total number of iterations reaches 2^64 at n ~ 4.8 million
*/
struct Index {
int i, j, k;
constexpr Index() noexcept
: i(2), j(1), k(0)
{}
Index& operator++() noexcept
{
if(k + 1 < j) {
++k;
return *this;
}
k = 0;
if(j + 1 < i) {
++j;
return *this;
}
j = 0;
++i;
return *this;
}
};
/**
* Padds Index to power of 2 alignment up to 16 byte
*
* This improves atomic operation performance because it avoids
* split-locks. Not sure if GCC's std::atomic makes actual use of this
* but clang does.
*/
struct AlignedIndex
{
private:
static constexpr std::size_t alignment =
sizeof(Index) < 2 ? 1 :
sizeof(Index) < 3 ? 2 :
sizeof(Index) < 5 ? 4 :
sizeof(Index) < 9 ? 8 :
16;
public:
union {
std::aligned_storage<sizeof(Index), alignment>::type pod;
Index index;
};
constexpr AlignedIndex() noexcept
: index()
{}
};
Index increment(std::atomic<AlignedIndex>& index) noexcept
{
AlignedIndex last = index.load(std::memory_order_relaxed);
AlignedIndex next;
do {
next = last;
++next.index;
} while(! index.compare_exchange_weak(last, next, std::memory_order_relaxed));
return last.index;
}
int main()
{
std::atomic<AlignedIndex> index(AlignedIndex{});
int n = 5;
for(Index cur; (cur = increment(index)).i < n; ) {
std::printf("%d %d %d\n", cur.i, cur.j, cur.k);
}
}
不是从 1..binom(n, 3) 迭代,而是从 1..n^3 迭代(概念上是数字集 1..n 的笛卡尔积与自身 2x,而不是3 个元素的组合,不重复)。这样做,我们可以很容易地从 M:
计算出 i/j/k
k = (M / N^0) % N = M % N
j = (M / N^1) % N
i = (M / N^2) % N = M / N^2
当然,这会导致重复,但我们不会一一跳过重复项。一旦我们达到 k>=j 处的数字,我们需要将 b 递增 (N-k)*N^0 = N-k 以使其再次“环绕”到 0。 j>=i 也是如此 - 将 b 递增 (N-j)*N^1,以环绕。
在这样做的过程中,我们回到了原始数字集。除法和模数计算有一些开销,每个变量最多可以重复一次(减去第一个变量),所以是的,有一些开销,但对于恒定数量的变量,它是常数。
再一次解决您的问题。正如评论中所说,您正在寻找的基本上是找到后继者和组合的排名。为此,我使用了 Kreher 和 Stinson 'Combinatorial algorithms' 一书中的算法。
这里是对应的代码,由next和unrank这两个函数组成,还有一个二项式系数的辅助函数,这是unranking函数所需要的:
int binomial ( int n, int k )
{
int mn = k;
if ( n - k < mn )
{
mn = n - k;
}
if ( mn < 0 ) { return 0; }
if ( mn == 0 ) { return 1; }
int mx = k;
if ( mx < n - k )
{
mx = n - k;
}
int value = mx + 1;
for (int i = 2; i <= mn; ++i)
{
value = ( value * ( mx + i ) ) / i;
}
return value;
}
auto unrank(int rank, int n, int k)
{
std::vector<int> t(k);
int x = 1;
for (int i = 0; i < k; ++i)
{
while (true)
{
int b = binomial ( n - x, k - i - 1);
if (b > rank) break;
rank -= b;
++x;
}
t[i] = x;
++x;
}
return t;
}
auto next(std::vector<int>& index, int n, int k)
{
for (int i = k-1; i >= 0; --i)
{
if (index[i] < n - (k-1) + i)
{
++index[i];
for (int j = i+1; j < k; ++j)
{
index[j] = index[j-1]+1;
}
return true;
}
}
return false;
}
想法是从给定的起始地址生成初始索引配置,然后计算该索引的后继 (end-start) 次。这是一个例子:
int main()
{
int n = 7;
int k = 4;
int start = 3;
int end = 10;
auto index = unrank(start,n,k);
auto print_index = [&]()
{
for(auto const& ind : index)
{
std::cout<<ind<<" ";
}
std::cout<<std::endl;
};
print_index();
for(int i=start; i<end; ++i)
{
next(index, n, k);
print_index();
}
}
打印
1 2 3 7
1 2 4 5
1 2 4 6
1 2 4 7
1 2 5 6
1 2 5 7
1 2 6 7
1 3 4 5
这里是 Demo。享受吧!
这是另一个基于Dillon Davis 的解决方案。
auto divide = [](float pos, int len) -> float {
auto n = static_cast<float>(len);
if (pos == 1) {
return n;
}
if (pos == 0) {
return 0;
}
// solve x * (x - 1) * (x - 2) = n * (n - 1) * (n - 2) * pos for x
// https://en.wikipedia.org/wiki/Bisection_method
float d = n * (n - 1) * (n - 2) * (1 - pos);
auto f = [d](float x) {
return std::pow(x, 3) - 3 * std::pow(x, 2) + 2 * x - d;
};
float a = 0;
float b = n;
float epsilon = 0.1f;
float x = 0;
while (std::abs(a - b) > epsilon) {
x = (a + b) / 2;
if (std::abs(f(x)) <= epsilon) {
break;
} else if (f(x) * f(a) < 0) {
b = x;
} else {
a = x;
}
}
return std::ceil(n - x);
};
速度非常快且开销极小,但不如 的解决方案准确,后者允许将 'work' 分成相等的部分。
示例:
auto testRun = [](int begin, int end, int n) {
int counter = 0;
for (int i = begin; i < end; ++i) {
for (int j = i + 1; j < n; ++j) {
for (int k = j + 1; k < n; ++k) {
++counter;
}
}
}
std::cout << counter << "\n";
};
int n = 1200;
int ranges = 4;
for (int i = 0; i < ranges; ++i) {
auto begin = static_cast<int>(divide((float) i / (float) ranges, n));
auto end = static_cast<int>(divide((float) (i + 1) / (float) ranges, n));
testRun(begin, end, n);
}
输出:
72035920
71897080
71619380
71728020
我正在研究一些繁重的算法,现在我正试图让它成为多线程的。它有一个带有 2 个嵌套循环的循环:
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; ++j) {
for (int k = j + 1; k < n; ++k) {
function(i, j, k);
}
}
}
我知道,function 次调用的次数将等于
但我还有最后一个问题:我不知道如何根据 b (0 <= b < binom(n, 3) 计算 i、j 和 k )
for (int b = start; b < end; ++b) {
// how to calculate i, j, k?
}
如何计算这些值?
编辑: 我的主要想法是从不同的线程调用这样的函数:
void calculate(int start, int end) {
for (int b = start; b < end; ++b) {
int i = ...;
int j = ...;
int k = ...;
function(i, j, k);
}
}
int total = binom(n, 3);
// thread A:
calculate(0, total / 2);
// thread B:
calculate(total / 2, total);
第三次尝试:
我已经获取了您的代码,并最终将其正确地发送到 运行(在 python 中):
def get_k(n):
total = 0
for i in range(3, n):
for j in range(i + 1, n):
for k in range(j + 1, n):
total += 1
V = total // 2 # for 2 threads
V_tmp = 0
for i in range(3, n):
if(V_tmp > V):
return i
for j in range(i + 1, n):
for k in range(j + 1, n):
V_tmp += 1
def pseudo_thread(start, end, n):
counter = 0
for i in range(start, end):
for j in range(i + 1, n):
for k in range(j + 1, n):
counter += 1
print(counter)
n = 145
k = get_k(n)
pseudo_thread(3, k, n)
pseudo_thread(k, n, n)
这应该最终会给你一个相对较好的拆分。即使 n=145,我们的计数器值也会得到 239260 和 227920。这显然不是一个优雅的解决方案,也不完美,但它在没有太多参考详细数学的情况下给了你正确的答案。
在 multi_index 的 class,它基本上可以满足您的需求,即
for(auto m : multi_index(3,3,4))
{
// now m[i] holds index of i-th loop
// m[0] goes from 0 to 2
// m[1] goes from 0 to 2
// m[2] goes from 0 to 3
std::cout<<m[0]<<" "<<m[1]<<" "<<m[2]<<std::endl;
}
但是,此代码仅适用于“正常”循环,其中每个维度从 0 到某个上限值。
在这个 post 中,我将尝试将其应用于反对称情况,其中 m[i]<m[j] 对应 i<j。链接代码的基本思想保持不变,即创建一个 class 来保存循环边界并提供可与基于范围的 for 循环一起使用的迭代器。唯一的区别是我使用 std::vector 而不是 std::array 作为索引数组类型:
#include <iostream>
#include <numeric>
#include <vector>
struct antisym_index_t
{
int upper_index;
int dim;
antisym_index_t(int upper_index, int dim) : upper_index(upper_index), dim(dim) {}
struct iterator
{
struct sentinel_t {};
int upper_index;
int dim;
std::vector<int> index_array = {};
bool _end = false;
iterator(int upper_index, int dim) : upper_index(upper_index), dim(dim), index_array(dim)
{
std::iota(std::begin(index_array), std::end(index_array),0);
}
auto& operator++()
{
for (int i = dim-1;i >= 0;--i)
{
if (index_array[i] < upper_index - 1 - (dim-1-i))
{
++index_array[i];
for (int j = i+1;j < dim;++j)
{
index_array[j] = index_array[j-1]+1;
}
return *this;
}
}
_end = true;
return *this;
}
auto& operator*()
{
return index_array;
}
bool operator!=(sentinel_t) const
{
return !_end;
}
};
auto begin() const
{
return iterator{ upper_index, dim };
}
auto end() const
{
return typename iterator::sentinel_t{};
}
};
auto antisym_index(int upper_index, int dim)
{
return antisym_index_t(upper_index, dim);
}
但是请注意,此代码到目前为止未经测试(写在我的头上)。您可以将其用作
for(auto m : antisym_index(5,3))
{
// now m[i] holds index of i-th loop
std::cout<<m[0]<<" "<<m[1]<<" "<<m[2]<<std::endl;
}
编辑:到目前为止,我已经测试并更正了代码,请参阅 here。给自己的备忘录:不要发布未经测试的代码。
EDIT2:顺便说一句,这在问题中回答了你的问题。我不清楚这对多任务处理有何帮助。
我没有完整的答案,但有 2 个循环的解决方案。我睡眠不足的头脑无法将其概括为 3 个循环,但也许其他人可以。
在 2D 中,问题变成了从展平索引中计算出三角矩阵的行和列索引。这使得很容易看出“逐渐变细”的一端包含在较大的一端中。在 ASCII 艺术中是这样的:
n
___________
|_ |
| |_ |
| |_ |
| | |_ |
| | |_ |
|___|_____|_|
i ^
|
binom(n-i, 2)
所以,让我们定义
n循环结束索引(矩阵数rows/columns)i外循环计数器范围 [0, n)。如图所示:列索引j内循环计数器范围 [0, i)。如图:行索引自下而上a扁平循环计数器范围 [0, binom(n, 2))
然后i可以从binom(n, 2) - binom(n-i, 2) = a计算出来。通过 Wolfram Alpha 的一次往返行程给我们:
i = trunc(-0.5 * sqrt((1 - 2 n)**2 - 8 a) + n - 0.5).
截断(=转换为 int)“向下舍入”到最后一个完整列。所以行索引 j 可以从 as
j = a - (binom(n, 2) - binom(n-i, 2))j = a - i*(-i + 2 n - 1) / 2
根据您想要的并行化方式,您还可以使用原子结构并通过比较和交换操作实现迭代。大多数平台上都有一个 16 字节的 CAS。 Link 与 -latomic 在 GCC 上。如果我们确保正确对齐,Clang 会内联 CAS 调用。
#include <atomic>
#include <type_traits>
#include <cstdio>
/**
* Index for a nested loop
*
* Index for loop in style
* for(i = 0; i < n; ++i)
* for(j = 0; j < i; ++j)
* for(k = 0; k < j; ++k);
*
* The total number of iterations is binom(n, 3)
*
* Indices are int for two reasons:
* 1. Keep overall size at or below 16 byte to allow atomic operations
* 2. The total number of iterations reaches 2^64 at n ~ 4.8 million
*/
struct Index {
int i, j, k;
constexpr Index() noexcept
: i(2), j(1), k(0)
{}
Index& operator++() noexcept
{
if(k + 1 < j) {
++k;
return *this;
}
k = 0;
if(j + 1 < i) {
++j;
return *this;
}
j = 0;
++i;
return *this;
}
};
/**
* Padds Index to power of 2 alignment up to 16 byte
*
* This improves atomic operation performance because it avoids
* split-locks. Not sure if GCC's std::atomic makes actual use of this
* but clang does.
*/
struct AlignedIndex
{
private:
static constexpr std::size_t alignment =
sizeof(Index) < 2 ? 1 :
sizeof(Index) < 3 ? 2 :
sizeof(Index) < 5 ? 4 :
sizeof(Index) < 9 ? 8 :
16;
public:
union {
std::aligned_storage<sizeof(Index), alignment>::type pod;
Index index;
};
constexpr AlignedIndex() noexcept
: index()
{}
};
Index increment(std::atomic<AlignedIndex>& index) noexcept
{
AlignedIndex last = index.load(std::memory_order_relaxed);
AlignedIndex next;
do {
next = last;
++next.index;
} while(! index.compare_exchange_weak(last, next, std::memory_order_relaxed));
return last.index;
}
int main()
{
std::atomic<AlignedIndex> index(AlignedIndex{});
int n = 5;
for(Index cur; (cur = increment(index)).i < n; ) {
std::printf("%d %d %d\n", cur.i, cur.j, cur.k);
}
}
不是从 1..binom(n, 3) 迭代,而是从 1..n^3 迭代(概念上是数字集 1..n 的笛卡尔积与自身 2x,而不是3 个元素的组合,不重复)。这样做,我们可以很容易地从 M:
计算出 i/j/kk = (M / N^0) % N = M % N
j = (M / N^1) % N
i = (M / N^2) % N = M / N^2
当然,这会导致重复,但我们不会一一跳过重复项。一旦我们达到 k>=j 处的数字,我们需要将 b 递增 (N-k)*N^0 = N-k 以使其再次“环绕”到 0。 j>=i 也是如此 - 将 b 递增 (N-j)*N^1,以环绕。
在这样做的过程中,我们回到了原始数字集。除法和模数计算有一些开销,每个变量最多可以重复一次(减去第一个变量),所以是的,有一些开销,但对于恒定数量的变量,它是常数。
再一次解决您的问题。正如评论中所说,您正在寻找的基本上是找到后继者和组合的排名。为此,我使用了 Kreher 和 Stinson 'Combinatorial algorithms' 一书中的算法。
这里是对应的代码,由next和unrank这两个函数组成,还有一个二项式系数的辅助函数,这是unranking函数所需要的:
int binomial ( int n, int k )
{
int mn = k;
if ( n - k < mn )
{
mn = n - k;
}
if ( mn < 0 ) { return 0; }
if ( mn == 0 ) { return 1; }
int mx = k;
if ( mx < n - k )
{
mx = n - k;
}
int value = mx + 1;
for (int i = 2; i <= mn; ++i)
{
value = ( value * ( mx + i ) ) / i;
}
return value;
}
auto unrank(int rank, int n, int k)
{
std::vector<int> t(k);
int x = 1;
for (int i = 0; i < k; ++i)
{
while (true)
{
int b = binomial ( n - x, k - i - 1);
if (b > rank) break;
rank -= b;
++x;
}
t[i] = x;
++x;
}
return t;
}
auto next(std::vector<int>& index, int n, int k)
{
for (int i = k-1; i >= 0; --i)
{
if (index[i] < n - (k-1) + i)
{
++index[i];
for (int j = i+1; j < k; ++j)
{
index[j] = index[j-1]+1;
}
return true;
}
}
return false;
}
想法是从给定的起始地址生成初始索引配置,然后计算该索引的后继 (end-start) 次。这是一个例子:
int main()
{
int n = 7;
int k = 4;
int start = 3;
int end = 10;
auto index = unrank(start,n,k);
auto print_index = [&]()
{
for(auto const& ind : index)
{
std::cout<<ind<<" ";
}
std::cout<<std::endl;
};
print_index();
for(int i=start; i<end; ++i)
{
next(index, n, k);
print_index();
}
}
打印
1 2 3 7
1 2 4 5
1 2 4 6
1 2 4 7
1 2 5 6
1 2 5 7
1 2 6 7
1 3 4 5
这里是 Demo。享受吧!
这是另一个基于Dillon Davis
auto divide = [](float pos, int len) -> float {
auto n = static_cast<float>(len);
if (pos == 1) {
return n;
}
if (pos == 0) {
return 0;
}
// solve x * (x - 1) * (x - 2) = n * (n - 1) * (n - 2) * pos for x
// https://en.wikipedia.org/wiki/Bisection_method
float d = n * (n - 1) * (n - 2) * (1 - pos);
auto f = [d](float x) {
return std::pow(x, 3) - 3 * std::pow(x, 2) + 2 * x - d;
};
float a = 0;
float b = n;
float epsilon = 0.1f;
float x = 0;
while (std::abs(a - b) > epsilon) {
x = (a + b) / 2;
if (std::abs(f(x)) <= epsilon) {
break;
} else if (f(x) * f(a) < 0) {
b = x;
} else {
a = x;
}
}
return std::ceil(n - x);
};
速度非常快且开销极小,但不如
示例:
auto testRun = [](int begin, int end, int n) {
int counter = 0;
for (int i = begin; i < end; ++i) {
for (int j = i + 1; j < n; ++j) {
for (int k = j + 1; k < n; ++k) {
++counter;
}
}
}
std::cout << counter << "\n";
};
int n = 1200;
int ranges = 4;
for (int i = 0; i < ranges; ++i) {
auto begin = static_cast<int>(divide((float) i / (float) ranges, n));
auto end = static_cast<int>(divide((float) (i + 1) / (float) ranges, n));
testRun(begin, end, n);
}
输出:
72035920
71897080
71619380
71728020